ISO 6976-16

Compression Factor

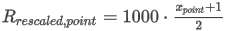
where the summation is taken over all N components of the mixture and:

Z(t₂,p₂) is the compression factor at metering temperature t₂ and metering pressure p₂

p₀ is the atmospheric pressure (101.325 kPa)

p₂ is the metering pressure

x_j is the mole fraction of component j

s(t₂,p₀) is the summation factor for component j at metering temperature t₂ and atmospheric pressure p₀

Mean Molecular Weight

where the summation is taken over all N components of the mixture and:

M is the mean molecular weight

x_j is the mole fraction of component j

M_j is the molar mass of component j

Gross Calorific Value

Molar basis (real gas property is calculated as ideal)

where the summation is taken over all N components of the mixture and:

(Hc)⁰_G(t₁) is the ideal molar gross calorific value of the mixture at combustion temperature t₁

[(Hc)⁰_G]_j(t₁) is the ideal molar gross calorific value of the component j at combustion temperature t₁

x_j is the mole fraction of component j

Mass basis (real gas property is calculated as ideal)

where:

(Hm)⁰_G(t₁) is the ideal mass gross calorific value of the mixture at combustion temperature t₁

(Hc)⁰_G(t₁) is the ideal molar gross calorific value of the mixture at combustion temperature t₁

M is the mean molecular weight

Volumetric basis - ideal gas

where:

(Hv)⁰_G(t₁;t₂,p₂) is the ideal volumetric gross calorific value of the mixture at combustion temperature t₁

(Hc)⁰_G(t₁) is the ideal molar gross calorific value of the mixture at combustion temperature t₁

p₂ is the metering pressure

R is the molar gas constant

T₂ is the absolute metering temperature in kelvins

Volumetric basis - real gas

where:

(Hv)_G(t₁;t₂,p₂) is the real volumetric gross calorific value of the mixture at combustion temperature t₁

Net Calorific Value

Molar basis (real gas property is calculated as ideal)

where the summation is taken over all N components of the mixture and:

(Hc)⁰_N(t₁) is the ideal molar net calorific value of the mixture at combustion temperature t₁

(Hc)⁰_G(t₁) is the ideal molar gross calorific value of the mixture at combustion temperature t₁

x_j is the mole fraction of component j

b_j is the hydrogen index of component j

L⁰(t₁) is the standard enthalpy of vaporization of water at combustion temperature t₁

Mass basis (real gas property is calculated as ideal)

where:

(Hm)⁰_N(t₁) is the ideal mass net calorific value of the mixture at combustion temperature t₁

(Hc)⁰_N(t₁) is the ideal molar net calorific value of the mixture at combustion temperature t₁

M is the mean molecular weight

Volumetric basis - ideal gas

where:

(Hv)⁰_N(t₁;t₂,p₂) is the ideal volumetric net calorific value of the mixture at combustion temperature t₁

(Hc)⁰_N(t₁) is the ideal molar net calorific value of the mixture at combustion temperature t₁

p₂ is the metering pressure

R is the molar gas constant

T₂ is the absolute metering temperature in kelvins

Volumetric basis - real gas

where:

(Hv)_N(t₁;t₂,p₂) is the real volumetric net calorific value of the mixture at combustion temperature t₁

Relative Density

Ideal gas

where:

G⁰ is the relative density of the ideal gas

M is the mean molecular weight

M_air is the molar mass of dry air of standard composition (28.96546 kg·kmol^-1)

Real gas

where:

G(t₂,p₂) is the relative density of the real gas at t₂ and p₂

Z(t₂,p₂) is the compression factor of the gas mixture at t₂ and p₂

Z_air(t₂,p₂) is the compression factor of dry air of standard composition at t₂ and p₂ calculated as:

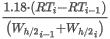
where Z_air(t₂,p₀) is the compression factor of the dry air of standard composition at t₂ and p₀

Density

Ideal gas

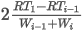
where:

D⁰(t₂,p₂) is the density of the ideal gas at t₂ and p₂

M is the mean molecular weight

R is the molar gas constant

T₂ is the absolute metering temperature in kelvins

Real gas

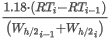
where:

D(t₂,p₂) is the density of the real gas at t₂ and p₂

Z(t₂,p₂) is the compressibility factor of the gas mixture at t₂ and p₂

Wobbe Index (Gross and Net)

Ideal gas

where:

W⁰_G/N(t₁;t₂,p₂) is the gross or net Wobbe index of the ideal gas at combustion temperature t₁

(Hv)⁰_G/N(t₁;t₂,p₂) is the ideal volumetric gross or net calorific value of the mixture at combustion temperature t₁

G⁰ is the relative density of the ideal gas

Real gas

where:

W_G/N(t₁;t₂,p₂) is the gross or net Wobbe index of the real gas at combustion temperature t₁

(Hv)_G/N(t₁;t₂,p₂) is the real volumetric gross or net calorific value of the mixture at combustion temperature t₁

G is the relative density of the real gas

ISO 6976-95

Compression Factor

where the summation is taken over all N components of the mixture and:

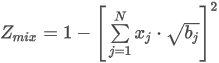
Z_mix is the compression factor

x_j is the mole fraction of component j

√b_j is the summation factor for component j

Mean Molecular Weight

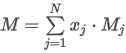
where the summation is taken over all N components of the mixture and:

M is the mean molecular weight

x_j is the mole fraction of component j

M_j is the molar mass of component j

Superior and Inferior Calorific Value

Molar basis (real gas property is calculated as ideal)

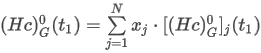
where the summation is taken over all N components of the mixture and:

H⁰(t₁) is the ideal molar calorific value of the mixture (superior or inferior)

H_j⁰(t₁) is the ideal molar calorific value of the component j (superior or inferior)

x_j is the mole fraction of component j

Mass basis (real gas property is calculated as ideal)

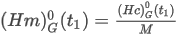
where:

Ĥ⁰(t₁) is the ideal calorific value on a mass basis of the mixture (superior or inferior)

H⁰(t₁) is the ideal molar calorific value of the mixture (superior or inferior)

M is the mean molecular weight

Volumetric basis - ideal gas

where:

H̃⁰[t₁,V(t₂,p₂)] is the ideal calorific value on a volumetric basis, for a combustion temperature t₁, of the mixture (superior or inferior), metered at a temperature t₂ and pressure p₂

H⁰(t₁) is the ideal molar calorific value of the mixture (superior or inferior)

R is the molar gas constant

T₂ is the absolute temperature in kelvins

Volumetric basis - real gas

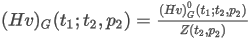
where:

H[t₁,V(t₂,p₂)] is the real-gas calorific value on a volumetric basis, for a combustion temperature t₁, of the mixture (superior or inferior), metered at a temperature t₂ and pressure p₂

Z_mix(t₂,p₂) is the compression factor at the metering reference conditions

Relative Density

Ideal gas

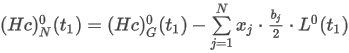
where the summation is taken over all N components of the mixture and:

d⁰ is the relative density of the ideal gas

M_j is the molar mass of component j

M_j is the molar mass of dry air of standard composition

Real gas

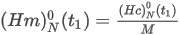
where the summation is taken over all N components of the mixture and:

d is the relative density of the real gas

Z_mix is the compression factor of the gas mixture

Z_air is the compression factor of dry air of standard composition

Density

Ideal gas

where the summation is taken over all N components of the mixture and:

ρ⁰(t,p) is the density of the ideal gas

R is the molar gas constant

T is the absolute temperature in kelvins

x_j is the mole fraction of component j

M_j is the molar mass of component j

Real gas

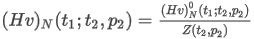
where:

ρ(t,p) is the density of the real gas

Z_mix is the compressibility factor of the gas mixture

Wobbe Index

Ideal gas

where:

W⁰[t₁,V(t₂,p₂)] is the Wobbe index of the ideal gas

H_S⁰[t₁,V(t₂,p₂)] is the superior calorific value on a volumetric basis, for a combustion temperature t₁, of the ideal gas, metered at a temperature t₂ and pressure p₂

d⁰ is the relative density of the ideal gas

Real gas

where:

W[t₁,V(t₂,p₂)] is the Wobbe index of the real gas

H̃_S[t₁,V(t₂,p₂)] is the superior calorific value on a volumetric basis, for a combustion temperature t₁, of the real gas, metered at a temperature t₂ and pressure p₂

d(t₂,p₂) is the relative density of the real gas

ASTM D 3588-98 and GPA 2172-09

Molar Mass

where the summation is taken over all N components of the mixture and:

M is the molar mass of the mixture

x_j is the mole fraction of component j

M_j is the molar mass of component j

Molar Mass Ratio

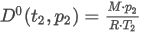
where the summation is taken over all N components of the mixture and:

G^id is the molar mass ratio of the mixture

x_j is the mole fraction of component j

G_j^id is the molar mass ratio of the compound j

M is the molar mass of the mixture

M_a is the molar mass of air

Compressibility Factor

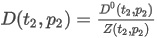
where the summation is taken over all N components of the mixture and:

Z(T,P) is the compression factor

P is the pressure

x_j is the mole fraction of component j

√β_j is the summation factor for component j

Relative Density

Ideal gas

where:

d^id is the relative density of the ideal gas

M is the molar mass of the mixture

M_a is the molar mass of air

Real gas

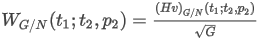
where:

d is the relative density of the real gas

Z is the compression factor of the gas mixture

Z_a is the compression factor of dry air

M is the molar mass of the mixture

M_a is the molar mass of air

Heating Value

According to ASTM D 3588-98, the real heating value is not given by division of the ideal heating value by the compressibility factor (Z). Real gas heating values differ from the ideal gas values by less than the order of the accuracy of the heating values. Thus, the real heating value is calculated as ideal. Furthermore, according to GPA 2172-09, dividing the ideal volumetric heating value by the compressibility factor provides the energy transferred in an ideal gas reaction per volume of real gas fuel (in Clarity, printed as Ideal Heating Value per Real Gas Volume).

Molar basis

where the summation is taken over all N components of the mixture and:

H_n^id is the heating value of the gas mixture on molar basis (gross or net)

x_j is the mole fraction of component j

H_n,j^id is the molar heating value of component j (gross or net)

Mass basis

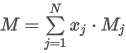
where the summation is taken over all N components of the mixture and:

H_m^id is the heating value of the gas mixture on mass basis (gross or net)

x_j is the mole fraction of component j

M_j is the molar mass of component j

H_m,j^id is the heating value per unit mass of component j (gross or net)

Volumetric basis

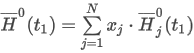
where the summation is taken over all N components of the mixture and:

H_V^id is the heating value of the gas mixture on volumetric basis (gross or net)

x_j is the mole fraction of component j

H_V,j^id is the heating value per unit volume of component j (gross or net)

ASTM D 2421-02 and D 2598-02

Vapor Pressure

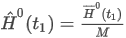
where the summation is taken over all N components of the mixture and:

p_V is the liquified petroleum (LP) gas vapor pressure of the sample at 37.8 °C

x_V,j is the liquid volume percent of component j in the mixture

vp_j' is the vapor pressure factor of component j at 37.8 °C

Relative density

where the summation is taken over all N components of the mixture and:

d is the relative density of the mixture

x_V,j is the liquid volume percent of component j in the mixture

sg_j' is the relative density of component j at 15.6 °C

Motor Octane Number

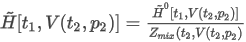
where the summation is taken over all N components of the mixture and:

MON is the calculated motor octane number of the mixture

x_V,j is the liquid volume percent of component j in the mixture

mon_j is the motor octane number of component j

ISO 8973-97 and EN 589+A1

Density

where the summation is taken over all N components of the mixture and:

ρ is the density of the mixture at 15 °C

ρ_j is the density factor of component j in the mixture at 15 °C

W_j' is the mass fraction of component j in the mixture, calculated as:

where the summation is taken over all N components of the mixture and:

x_j is the mole fraction of component j

M_j is the relative molecular mass of component j

Absolute Vapor Pressure

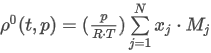
where the summation is taken over all N components of the mixture and:

p_v is the absolute vapor pressure of the LPG sample

x_j is the mole fraction of component j in the mixture

p_v,j is the vapor pressure factor of component j

Gauge Vapor Pressure

where:

p_ve is the gauge vapor pressure

Octane Number

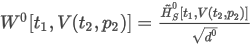
where the summation is taken over all N components of the mixture and:

ON is the calculated octane number of the mixture

x_j is the molar fraction of component j in the mixture

pon_j is the partial octane number of component j

Additional notes

Methane Number

According to KUBESH, John; KING, Steven R.; LISS, William E. Effect of gas composition on octane number of natural gas fuels. SAE Technical Paper, 1992, equation (4):

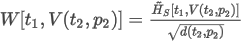
where:

MN is the calculated methane number of the mixture

ON is the octane number of the mixture

1.624 and 119.1 are the coeficients obtained via regression as described in the Article

Calculation on wet basis

For calculations of gas properties on wet basis according to norms ISO 6976-95, ASTM D 3588-98, and GPA 2172-09, the mole fraction of water in natural gas saturated with water is added to the resulting NGA Amounts. For ASTM D 3588-980 and GPA 2172-09, the base temperature is defined as 60 °F (corresponding to the saturated mole fraction of water equal to 0.01744). In ISO 6976-95, the available metering temperatures are 0, 15, and 20 °C. The mole fractions of water vapor in saturated gas at these temperatures were calculated according to the following equation:

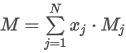
where:

x_w(T) is the mole fraction of water vapor in saturated gas at temperature T

p_atm is the atmospheric pressure (101.325 kPa).

p_sat(T) is the saturation vapor pressure of water at temperature T, obtained from the NIST database, Saturation water properties, P.J. Linstrom and W.G. Mallard, Eds., NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg MD, 20899, https://doi.org/10.18434/T4D303, (retrieved February 15, 2024).